Geometria Konstruado

Konstruado per Rektilo kaj Cirkelo

La matematikistoj de Antikva Grekio konigis la klasikan metodon de geometria konstruado. Ĉi tiu metodo uzas nur idealan rektilon kaj idealan cirkelon. Teore, la rektilo kaj la cirkelo povas longiĝi senlime kaj konstrui perfektajn rektajn liniojn kaj perfektajn arkojn sur Eŭklida surfaco. Ĝi baziĝas sur la aksiomoj de Eŭklida Geometrio, kiuj estas:

1. ajnaj du punktoj povas kunligiĝi per rekta linio;
2. ajna linio povas plilongiĝi nebarite;
3. por ajna linio, oni povas fari cirklon kun mezo en unu fino de la linio kaj kun radiuso, kiu egalas al longeco de ĝi;
4. ĉiuj ortaj anguloj estas kongruaj;
5. du linioj, kiuj tranĉas la trian tiel, ke la sumo de iliaj anguloj je unu flanko estas malpli ol du ortaj anguloj, tranĉiĝas je tiu flanko.

La Bazaj Konstruadoj

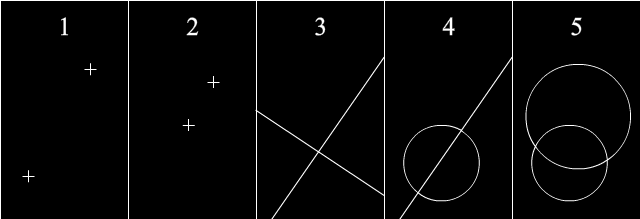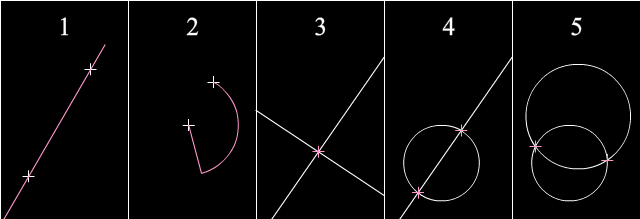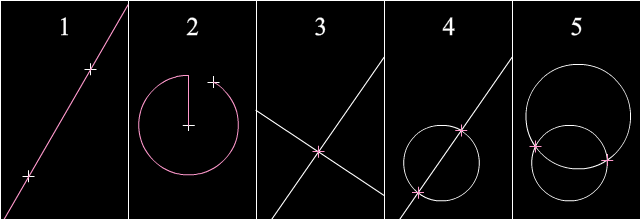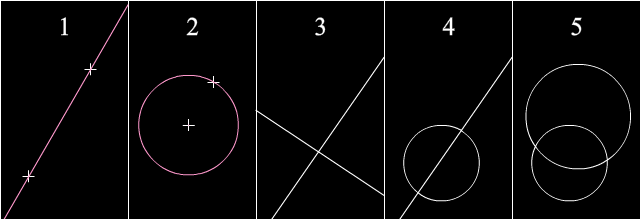
En ajna geometria konstruado, oni havas la komencajn punktojn, liniojn, kaj cirklojn. Poste, oni faras "algoritmon" per ĉi tiuj kvin bazaj konstruadoj por konstrui la finan konstruaĵon.

1. Oni povas desegni linion tra du punktoj.
2. Oni povas desegni cirklon tra unu punkto kun centro sur alia punkto.
3. Oni povas desegni punkton sur la loko, kie du linioj intersekcas.
4. Oni povas desegni unu aŭ du punktojn sur la loko, kie linio kaj cirklo intersekcas.
5. Oni povas desegni unu aŭ du punktojn sur la loko, kie du cirkloj intersekcas.

Konstrui Egalajn Cirklojn

Aktuale, oni ne eblas konservi distacon per movigi la cirkelon por desegni egalajn (kongruajn) cirklojn ĉar la cirkelo fermos post oni finas desegni la unuan cirklon. Tamen, la saman resulton oni povas atingi per ĉi tiu metodo. Ĝi estas la Teoremo de Cirkela Ekvivalenteco. Poste, mi rekte movigos la cirkelon por tiaj konstruadoj.

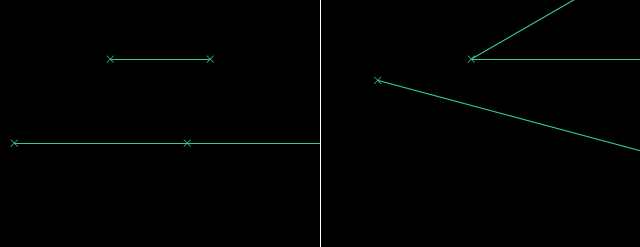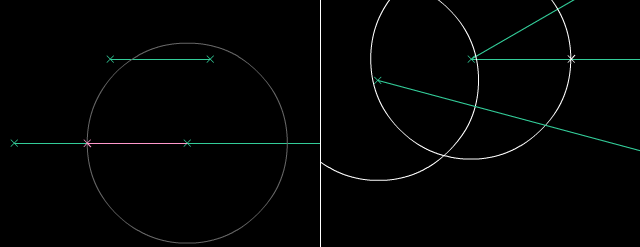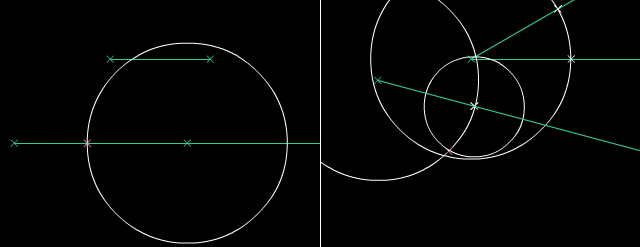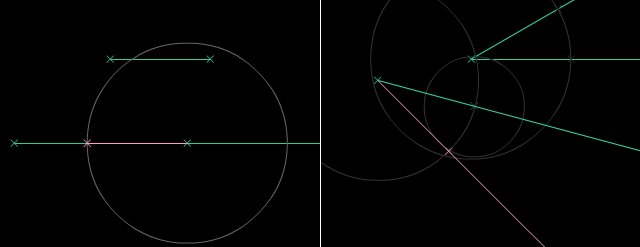
Per konservi distancon, nun oni povas konstrui egalajn liniojn. Per konservi du distancojn, oni ankaŭ povas konstrui egalajn angulojn. Poste, mi rekte kopios la linion kaj angulon por tiaj konstruadoj.

Nun, oni povas adici kaj subtrahi longojn. Oni ankaŭ povas adici kaj subtrahi angulojn. Pro tio, oni povas konstrui ajnan linion, kiu longas pozitivan entjeron (ekzemple 1, 2, 3, 4, aŭ tiaj aliaj nombroj; la unua linio longus 1 mezurunuon; poste oni povus adici tiun linion kun mem por konstrui novan linion, kiu longas 2 mezurunuon; poste 3 mezurunuon; kaj tiel plu).

Konstrui Ortajn Liniojn

Ortaj linioj (ankaŭ nomiĝas perpendiklaj linioj) estas linioj, kiu intersekcas unu la alian kun angulo 90° (kvarono de cirkl-perimetro, π/2 radio) sur Eŭklida surfaco. Per la maldekstra metodo, oni povas konstrui ortan linion tra la komenca punkto, kiu ne estas sur la komenca linio. Per la dekstra metodo, oni povas konstrui ortan linion tra la komenca punkto, kiu estas sur la komenca linio. Poste, mi rekte desegnos ortan linion por tiaj konstruadoj.

Konstrui Paralelajn Liniojn

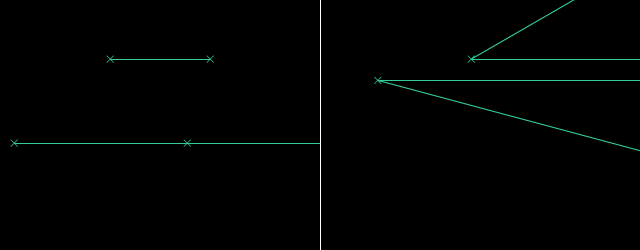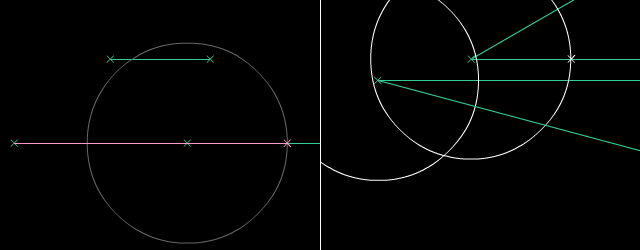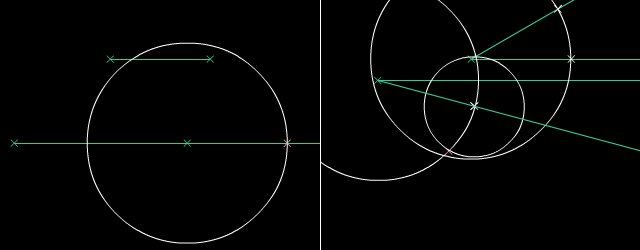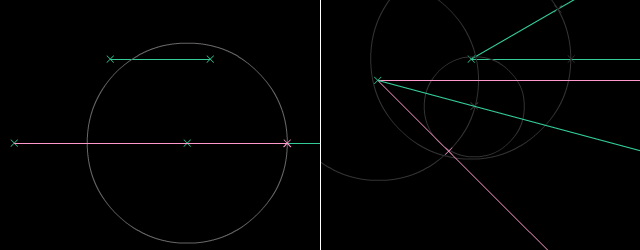
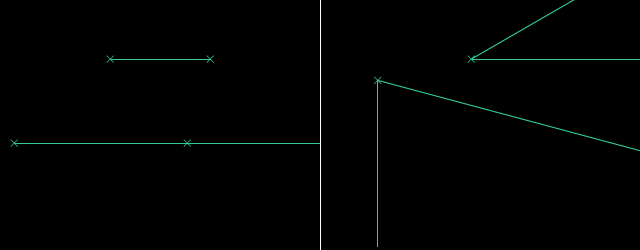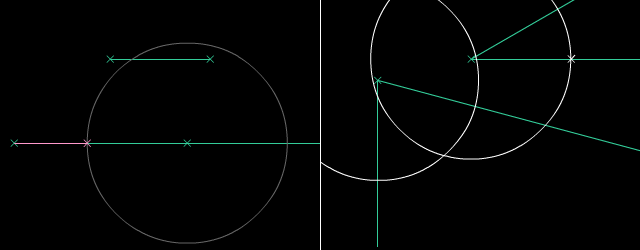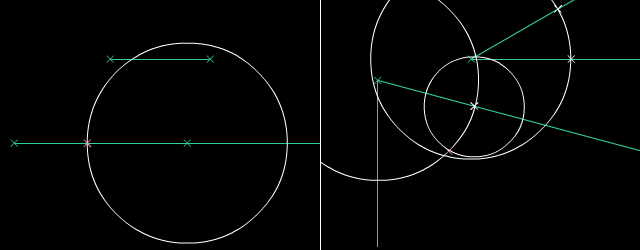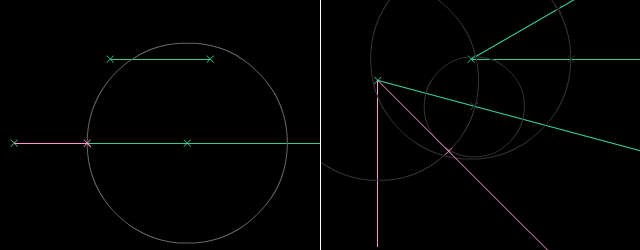
Paralelaj linioj estas linioj, kiuj neniam intersekcos unu la alian sur Eŭklida surfaco. Oni povas konstrui parelalan linion tra la komenca punkto per desegni du egalajn cirklojn. Oni uzas la Teoremo de Cirkela Ekvivalenteco por konstrui la du cirklojn. Poste, mi rekte desegnos paralelan linion por tiaj konstruadoj.

Dividi Liniojn

Oni povas duonigi ajnan linion sur Eŭklida surfaco. Tiu ĉi metodo ankaŭ konstruas ortan linion. Oni povas ĝeneraligi ĉi tion por trionigi, kvaronigi, aŭ dividi linion en iom ajn partojn. Poste, mi rekte dividos linion por tiaj konstruadoj.

Pro tio, oni povas dividi ajnan linion ajn iel. Pro la adicio de longoj per Teoremo de Cirkela Ekvivalenteco, oni jam povas konstrui linion, kiu longas ajnan povitivan entjron. Do nun oni ankaŭ povas konstrui linion, kiu longas ajnan povitivan racionalan nombron. Racionala nombro estas kvociento (dividaĵo) el du ne-nul entjeroj. Tiaj nombroj estas nomigeblaj per racio, kiel rilatumoj aŭ frakcionoj, ekzemple ¾ kaj 3,14.

Dividi Angulojn

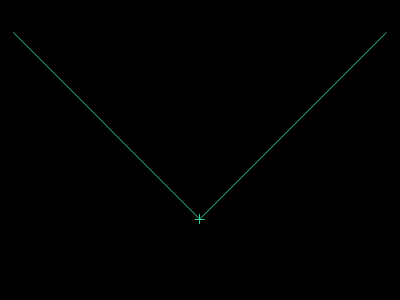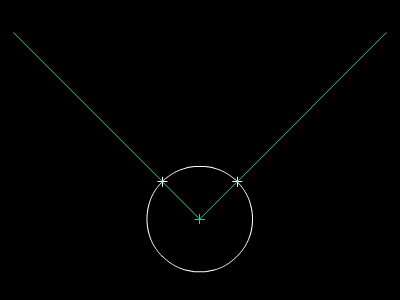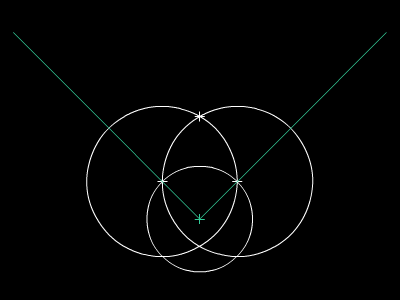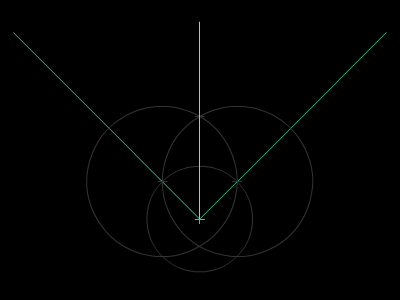
Oni povas duonigi ajnan angulon sur Eŭklida surfaco. Do oni povas konsrui ajnan angulon, kiu longas duonigaĵon de 360° (plena cirkl-perimetro, 2π radio) de Poste, mi rekte duonigos angulon por tiaj konstruadoj. La metodo de angul-duonigado similas la lini-duonigadon. Tamen, oni ne povas trionigi ajnan angulon per rektilo kaj cirkelo. Oni devas uzi metodon de konstruado per faldado por fari ĝin.

La Konstrueblaj Longoj

Pro la Teoremo de Pitagoro, oni povas ankaŭ fari la kvardatan radikon de ajnan longon per konstrui ortan triangulon. Oni ankau povas adicii, subtahi, multipliki, kaj dividi tiajn longojn per ajnaj aliaj longoj.

Do, oni nun povas fari ajnan linion, kiu longas tiom mezurunuon, kiom estas akirebla el la nombro 1 per adicio, subtraho, multipliko, divido, kaj kvardata radiko. Nombroj, kiuj estas akirebla per tiaj metodoj, nomiĝas konstrueblaj nombroj.

La Konstrueblaj Anguloj

Pro la angul-duonigado, oni povas konstrui angulojn, kiuj estas duonaĵoj de 360° (plena cirkl-perimetro, 2π radio). Pro la Teoremo de Pitagoro kaj trigonometrio, oni povas konstrui angulojn, kies tangentoj estas akirebla el pozitiva entjero per adicio, subtraho, multipliko, divido, kaj kvardata radiko (oni povas konstrui ortan triangulon el la konstrueblaj longoj).

reiras al la ĉefretpaĝo